WebGL - 3D im Browser
|
|
Home WebGL Api Spickzettel WebGL Sicherheit Tutorial 0 : WebGL Browser 1 : Das erste Dreieck 2 : 3D-Mathematik 3 : Farbe 4 : Animation 5 : Interaktion I 6 : Texturen 7 : Beleuchtung I 8 : Interaktion II Links WebGL Beispiele WebGL Frameworks ext. WebGL Tutorials Kontakt / Impressum webgl ([ät)] peter-strohm Punkt de |
8 Interaktion II>>>> Direkt zum Beispiel <<<<8.1 Worum geht's?Im Kapitel 5: Interaktion I habe ich beschrieben, wie man per Maus und Tastatur 3D-Objekte bzw. deren Darstellung rotiert und zoomt. Das ist zwar schon ganz nett, aber unter der Überschrift Interaktion erwartet man eigentlich etwas anderes: In den meisten 3D-Applikationen ist es möglich, einzelne Objekte aus einer 3D-Szene mit der Maus anzuklicken und dadurch in irgendeiner Weise zu verändern. Oder praktischer ausgedrückt: in einem 3D-CAD-Programm kann per Maus "Click-and-Drag" z.B. eine Bohrung in ein Bauteil modelliert werden, oder in einem Ego-Shooter kann ein Alien per MausklickIn diesem Tutorial soll es nun darum gehen, diese Art der Interaktion mit einer WebGL 3D-Szene in unseren Quellcode einzubauen. Diese Aufgabe hat wiedermal relativ viel mit räumlicher Geometrie zu tun. Egal, was die Anwendung hinterher sein soll, die entscheidende Frage ist: Wenn der User in der 2-dimensionalen Darstellung der 3-dimensionalen Szene auf einen Pixel klickt, welches Objekt (Dreieck) der 3D-Szene hat er damit angeklickt? 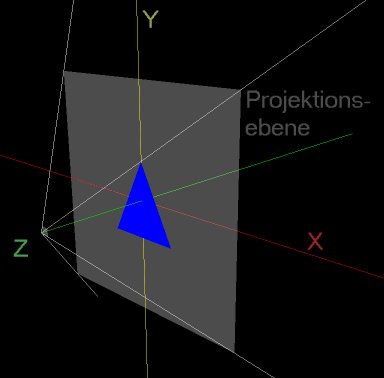 Bild 8.1 : Das Bildfeld, die Projektionsebene und das Koordinatensystem 8.2 Der "Klickstrahl"Eine wichtige Rolle spielt (wiedermal) die Projektionsebene, die hier in die X-Y-Ebene gelegt ist. Auf der Webseite entspricht die Projektionsebene der HTML-Canvas mit ihren 500 x 500 Pixeln. JavaScript bietet uns mit demonclick-Event einen leichten
Zugriff auf die x/y-Koordinate, die der User bei einem Mausklick getroffen hat.
und
Jezt müssen wir die Transformation der Canvas-Koordinaten in die 3D-Koordinaten vornehmen. Wenn wir sämtliche Rotationen und Translationen erstmal nicht berücksichtigen ist das auch nicht all zu schwierig: Die Kamera, der "Beginn" des Sichtraumes ist bei den Koordinaten X = 0m, Y = 0m und Z = 3m (in Bild 8.1 links unten); die Projektionsebene ist ein quadratischer Ausschnitt der X-Y-Ebene. (Ich bezeichne die Raumkoordinaten o.b.d.A. mit m für Meter; es können natürlich auch beliebige andere Einheiten sein, aber so ist es hoffentlich gut lesbar.) Der Öffnungswinkel des Sichtfelds ist auf 90° (45°nach links,rechts,oben,unten) festgelegt (vgl. Quellcode). Damit kann man über eine einfache tan-Beziehung berechnen, wie hoch und breit das Sichtfeld in der X-Y-Ebene ist: SichtfeldöffnungX-Y-Ebene = 3m × tan(45°) = 3m [8.1] Mit einem einfachen Dreisatz können wir damit auch ausrechnen, welchen Punkt in der X-Y-Ebene ein Mausklick des Users treffen würde: $\frac{X_{xyEbene}}{X_{canvas}} = \frac{Sichtfeldbreite}{Canvasbreite}$ bzw.$\frac{X_{xyEbene}}{X_{canvas}} = \frac{Sichtfeldhöhe}{Canvashöhe}$ (8.2) Unser eigentliches Ziel ist aber noch nicht erreicht: wir wollen nicht nur wissen welcher Punkt im 3D-Raum in der X-Y-Ebene getroffen würde, sondern allgemein in welche Richtung der Mausklick im Raum geht und welche Dreiecke von diesem "Klickstrahl" getroffen werden. 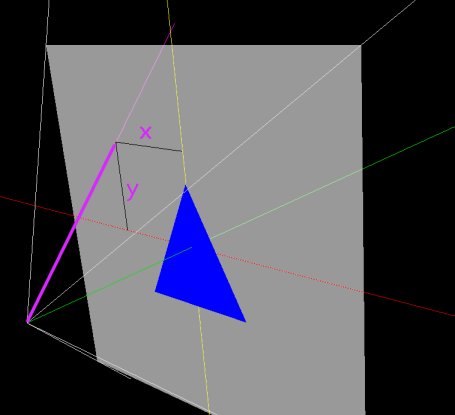 Bild 8.2 : Der "Klickstrahl" (violett) Mit der bereits geleisteten Vorarbeit können wir den "Klickstrahl", also den Strahl vom Punkt der virtuellen Kamera durch den Mausklick-Punkt ins Unendliche, gut bestimmen: Wir müssen lediglich eine Geradengleichung für eine Raumgerade aufstellen: $\overrightarrow{g}\left(s\right) = \overrightarrow{p} + s\cdot\overrightarrow{u}$(8.3) p : 3D-Stützvektor der Geraden, "Startpunkt" u : 3D-Richtungsvektor der Geraden s : Parameter Wir wissen, dass der "Klickstrahl" von der virtuellen Kamera ausgeht, d.h. wir können die Koordinaten dieser Kamera als Stützvektor verwenden: $\overrightarrow{p} = \left(\begin{array}{c}0 \\0 \\3 \end{array} \right) $ Weiterhin haben wir ein paar Zeilen weiter oben den Durchstoßpunkt des "Klickstrahls" durch die XY-Ebene berechnet und kennen damit einen zweiten Punkt für die Gerade. Aus der Differenz des Startpunktes und des Durchstoßpunktes können wir den Richtungsvektor berechnen: $\overrightarrow{u} = \left(\begin{array}{c}0 \\0 \\3 \end{array} \right) - \left(\begin{array}{c}X_xyEbene \\Y_xyEbene \\0 \end{array} \right) $ Üblicherweise und weil es der Veranschaulichung dient wird der Richtungsvektor u noch normiert, d.h. auf die Länge 1 gekürzt bzw. gestreckt. Das überlasse ich aber der sylvester.js -Bibliothek. 8.3 Getroffen oder daneben ?Im vorangegangenen Absatz haben wir den Klickstrahl berechnet, der von der Kamera ausgeht und durch einen Maus-Klickpunkt in die Tiefe des Raumes geht. Jezt geht es darum, die Frage zu beantworten, ob der Strahl ein bestimmtes Dreieck trifft oder daran vorbei geht.Ich stelle hier einen Algorithmus vor, der zwar relativ langsam ist, aber dafür relativ leicht verständlich. Im wesentlichen geht es um Fragestellungen der räumlichen Geometrie. Wir stellen zunächst die Normalenform der Ebene auf in der das Dreieck liegt. Danach berechnen wir den Schnittpunkt zwischen Klickstrahl und dieser Ebene. (Dieser ist immer vorhanden, solange Strahl und Ebene nicht parallel liegen). Sobald der Schnittpunkt berechnet ist, reduziert sich das Problem auf zwei Dimensionen. Bild 8.3 : Ist der (rote) Punkt innerhalb des Dreiecks, so ist die Winkelsumme der Verbindungen zwischen dem Klickpunkt und den Eckpunkten des Dreiecks gleich 360° (links im Bild). Liegt der Klickpunkt außerhalb des Dreiecks, wird diese Winkelsumme kleiner (rechts im Bild). Die Normalenform der Dreiecksebene lässt sich aus den Vektoren der drei Dreieckspunkte berechnen (mehr dazu in jedem guten Algebrabuch!) $E : \vec{n}\times\vec{x}+\vec{d}=0$ mit $\vec{n}=\frac{\left(\left(\vec{a}-\vec{b}\right)\times\left(\vec{a}-\vec{c}\right)\right)}{\left|\left(\left(\vec{a}-\vec{b}\right)\times\left(\vec{a}-\vec{c}\right)\right)\right|}$ (8.5) Bekanntermaßen ergibt das Kreuzprodukt zweier nicht paralleler Vektoren im $R^3$ einen Vektor der senkrecht auf beiden steht. Zwei Vektoren, die mit Sicherheit in der Dreiecksebene liegen, sind die Kantenvektoren die sich aus den Differenzen der Eckpunkt-Vektoren berechnen (a-b und a-c). Der Nenner des Bruches dient nur zur Normierung auf die Länge 1. Der Vektor d in Gleichung 8.4 kann leicht berechnet werden, indem man einen bekannten Punkt der Ebene (einen Dreieckspunkt) für x in die Gleichung einsetzt und nach d umstellt: $\vec{d}=-\left(\vec{n}\times\vec{x}_{p}\right)=-\left(\vec{n}\times\vec{a}\right)$ (8.6) Damit wären Klickstrahl und Ebene vollständig bekannt; Wir berechnen den Schnittpunkt der beiden, indem wir g(s) (Gleichung(8.3)) als x in (8.4) einsetzen und nach dem Parameter s auflösen: $E : \vec{n}\times\vec{g}\left(s\right)-\left(\vec{n}\times\vec{a}\right)=0$ (8.7) $E : \vec{n}\times\left(\vec{p}+s\cdot\vec{u}\right)-\left(\vec{n}\times\vec{a}\right)=0$ (8.8) umgestellt nach s: $E:\vec{n}\times\vec{p}+s\cdot\vec{n}\times\vec{u}-\vec{n}\times\vec{a}=0$ (8.9) $E : s=\frac{\vec{n}\times\vec{a}-\vec{n}\times\vec{p}}{\vec{n}\times\vec{u}}$ (8.10) Hier musst du beachten, dass s positiv sein muss, wenn der gesuchte Schnittpunkt im Sichtfeld liegen soll. Wir haben den Richtungsvektor des Klickstrahls so bestimmt, dass er VON der Kamera IN das Blickfeld hinein gerichtet ist. Wenn s negativ ist, wäre der Schnittpunkt hinter dem Betrachter bzw. hinter der virtuellen Kamera. Da wir nun (endlich) das Dreieck und den Schnittpunkt des Klickstrahls mit der DreiecksEBENE kennen, kommen wir jezt zur Frage, ob der Schnittpunkt innerhalb des Dreiecks liegt oder irgendwo sonst in dieser Ebene. Dazu hilft Bild 8.3 mehr als tausend Worte. Ist der Schnittpunkt innerhalb des Dreiecks, so ist die Winkelsumme der Verbindungen zwischen dem Schnittpunkt und den Eckpunkten des Dreiecks gleich 360° (links in Bild 8.3). Liegt der Schnittpunkt außerhalb des Dreiecks, wird diese Winkelsumme kleiner (rechts in Bild 8.3). Aufgrund von Rechengenauigkeit und Rundungsfehlern sollte man nicht GENAU 360° erwarten (359,982° kann auch bedeuten, dass der Punkt im Dreieck liegt). Wir brauchen also nur die Vektoren von den Eckpunkten des Dreiecks zu dem Schnittpunkt zu berechnen und anschließend die Winkel zwischen diesen Vektoren zu berechnen und zu addieren und voilá: wir wissen, ob der Mausklick das Dreieck getroffen hat!
Was jezt mit dieser Erkenntnis passieren soll, hängt natürlich von der Anwendung ab. In diesem Beispiel wird die Textur der Pyramide abwechslend verändert, wenn der Mausklick auf einem Dreieck erfolgte oder im leeren Raum. 8.4 Aus der Tiefe des Raumes...Klicks auf verschobene und rotierte DreieckeBisher habe ich die Themen Rotation und Translation in Bezug auf den Hit-Test ausgeblendet. Es drängt sich natürlich die Frage auf, wie rotierte und verschobene Dreiecke und Kamerapositionen sich auf die Frage "Getroffen oder daneben?" auswirken.Die Antwort ist so einfach wie ernüchternd: Translation und Rotation müssen genauso behandelt werden wie bei den Themen Projektion (Kapitel 2) und Beleuchtung (Kapitel 7). Alle Vertices und Normalen die in die Berechnung einfließen, müssen zuvor mit der aktuellen Modelview-Matrix bzw. der Normalenmatrix multipliziert werden. Die Herleitung der Normalenmatrix findest du in Kapitel 7. Die Gleichungen 8.5 - 8.10 werden dadurch etwas unübersichtlicher, was bei der Erklärung möglicherweise verwirrt hätte. Im Quellcode des Beispiels zu diesem Kapitel findest du natürlich alle erforderlichen Transformationen, so dass das Beispiel auch mit rotierter oder verschobener Pyramide funktioniert. 8.5 Der Hit-Test im QuellcodeDer Anfang dieses Tutorials war weitgehend unabhängig von WebGL/JavaScript; die gleichen Probleme und Lösungen beschäftigen Dich auch bei Direct3D, OpenGL und allen anderen 3D-Grafiksystemen.Alles was ich 8.1 - 8.4 erklärt habe, solltest Du in der Funktion hitTest(..) in kapitel8.html
wiedererkennen. Es waren noch ein paar Konvertierungen von 4D nach 3D erforderlich, die aber keine tiefere Bedeutung haben.Zwei weitere mittelgroße Veränderungen im Quellcode, die ich im Vergleich zu kapitel7.html vorgenommen habe, betreffen
nicht unmittelbar den Hit-Tests und sind in 8.6 und 8.7 erklärt.8.6 Dynamische Texturen mit der 2D-CanvasIn den Tutorials 6 (Texturen) und 7 (Beleuchtung I) haben wir jeweils Jpeg-Dateien als Texturen verwendet. Hier möchte ich eine andere Möglichkeit vorstellen (ja, gif, png u.a. funktionieren je nach Browser im Prinzip genauso wie Jpeg!!!).Das HTML5-Element <canvas>, das wir auch für den 3D-Inhalt verwenden, kann genauso gut (ehrlich gesagt sogar besser; danke Microsof IE >:-( ) für 2D-Grafiken verwendet werden. Die Syntax zum 2D-Zeichnen auf der Canvas ist nicht besonders spannend. Interessant wird es jedoch, wenn man eine solche 2D-Canvas als Textur im WebGL-Context verwendet. Eine solche Textur kann zur Laufzeit verändert werden, muss nicht aus einer zusätzlichen Datei nachgeladen werden und bietet eine gute Möglichkeit, Text (für Beschriftungen etc.) in die 3D-Welt einzubringen. Wenn du ganz mutig bist, kannst du noch weiter gehen, und auf diese Weise Videos oder sogar andere WebGL-Szenen als Texturen verwenden! In diesem Beispiel begnügen wir uns aber mit einer einfachen 2D-Canvas, die abhängig davon ob der vorangegangene Mausklick getroffen hat oder nicht, die Farbe wechselt und das Wort "rot" bzw. "blau" darstellt.  Bild 8.4 : die Texturen-Canvas in rot und in blau, jeweils 128x128 pixel Die Funktion initTexture wurde entsprechend modifiziert:
Die Funktion initTexture(..) wird von der Funktion HitTest(), also nach jedem Mausklick, aufgerufen.8.7 Dreiecke als JavaScript-ObjekteEine weitere Erweiterung des Quellcodes im Vergleich zum vorangegangenen Kapitel habe ich in Bezug auf die Handhabung der Vertices (3D-Punkte) vorgenommen.Bisher haben wir in der Funktion initBuffers(..) die Koordinatenlisten für Vertices und Normale immer ausgeschrieben:
var vertices = [
Bei der Pyramide aus vier Dreiecken geht das noch, aber du kannst dir leicht vorstellen, dass bei komplexeren 3D-Modellen nicht alle Koordinaten so in den Quellcode geschrieben werden (können)... Zunächst legen wir alle in dieser Szene vorkommenden 3D-Punkte in einem Array vom Typ Vector (aus Sylvester.js) ab.
Zu einer flexibleren Behandlung der Vertex- und Normalen-Arrays habe ich in glpsutilskap8.js
die JavaScript-Klasse IndexedVertexTriangle. Diese Klasse verwaltet Dreiecke anhand des Vektor-Array und der
zugehörigen Indizes speziell für dieses Dreieck.
Wie du (vielleicht) siehst, macht die Klasse IndexedVertexTriangle keine besonders komplizierten Dinge:
Sie speichert die drei Indizes der Dreieckspunkte bezogen auf das übergebene Vector-Array und hat außerdem noch zwei
Member-Funktionen, die es erleichtern sollen, auf die Dreiecksnormalen bzw. Eckpunkte zuzugreifen. Die Berechnung der Dreiecksnormalen geschieht wieder über das Kreuzprodukt zweier Kantenvektoren. Mit diesen Vorarbeiten können wir die eigentlichen Dreiecke nun folgendermaßen anlegen:
Danach wird in der Funktion initBuffers() der Grafikspeicher nun mit einer For-Schleife über alle (4) Dreiecke
initialisiert. (Für jedes Dreieck sind 3x3=9 Zahlenwerte erforderlich).Das sieht zwar bei unseren bescheidenen vier Dreiecken recht aufwändig aus (und deshalb führe ich diese Verbesserung auch erst in diesem Kapitel ein), dient aber enorm der Übersicht und Kompaktheit des Codes sobald mehr Dreiecke ins Spiel kommen. Das Füllen des vertexNormals-Arrays funktioniert nach dem gleichen Schema, deshalb gehe ich nicht nochmal darauf ein. Den Buffer der Texturkoordinaten füllen wir in diesem Kapitel noch auf konventionelle Art. 8.8 AusblickDieses Kapitel Interaktion II bietet eine sehr nützliche Basis für "echt" interaktive 3D-Anwendungen auf Basis von WebGL.Der Algorithmus den ich hier vorgestellt habe, um zu entscheiden ob ein Dreieck getroffen wurde oder nicht, ist anschaulich und funktioniert gut, aber leider nicht besonderes schnell. Die Winkelberechnungen sind zeitaufwändig und es gibt schnellere Verfahren, die jedoch weniger anschaulich sind. Wenn Du Bedarf an schnelleren Algorithmen hast, empfehle ich, mal nach dem Thema Kollisionserkennung bzw. Collision Detection zu suchen. Der HitTest ist nur ein kleiner Ausschnitt aus dem Bereich der Kollisionserkennung. Neben dem Berechnungsaufwand sind andere Arten der Kollision interessant und relevant: z.B. die Frage wann sich zwei Dreiecke im Raum schneiden muss beantwortet werden, wenn sich z.B. ein Avatar in einer 3D-Welt bewegt und nicht durch Wände und andere Figuren hindurch laufen können soll. Es bleibt spannend! ;-) |