WebGL - 3D im Browser
|
|
Home WebGL Api Spickzettel WebGL Sicherheit Tutorial 0 : WebGL Browser 1 : Das erste Dreieck 2 : 3D-Mathematik 3 : Farbe 4 : Animation 5 : Interaktion I 6 : Texturen 7 : Beleuchtung I 8 : Interaktion II Links WebGL Beispiele WebGL Frameworks ext. WebGL Tutorials Kontakt / Impressum webgl ([ät)] peter-strohm Punkt de |
7 Beleuchtung I>>>> Direkt zum Beispiel <<<<7.1 BeleuchtungsartenBeleuchtung ist der 3D-Grafik ist (beinahe) eine Wissenschaft für sich...Wir beginnen hier zunächst mit der einfachsten Art der simulierten Beleuchtung: Umgebungslicht und gerichtetes Licht (ambient und directional lighting in der englischsprachigen Literatur).Zur Veranschaulichung, wo es in diesem Kapitel hingehen soll, erst mal ein Bildchen: 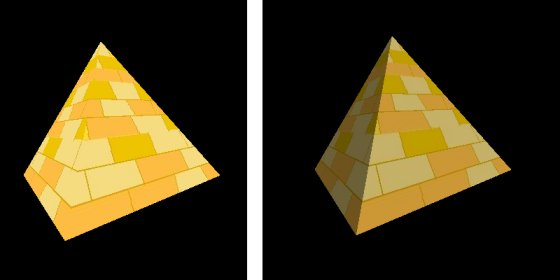 Bild 7.1 : Vergleich: Pyramide ohne und mit gerichteter Beleuchtung. Die Lichtquelle befindet sich im rechten Bild rechts oberhalb hinter dem Betrachter. Im rechten Teil von Bild 7.1 befindet sich eine gerichtete Lichtquelle (vgl. Sonne) rechts oberhalb hinter dem Betrachter und strahlt (ungefähr) senkrecht auf die Vorderseite der Pyramide. Die linke Seite wird nicht von der Lichtquelle beleuchtet. Das "Restlicht" das dafür sorgt, dass diese Pyramidenseite nicht völlig dunkel ist, ist das Umgebungfslicht (ambient light). In der Realität entsteht das Umgebungslicht durch unendliche viele diffuse Reflektionen der Lichtquelle (z.B. der Sonne) an Oberflächen der Umgebung. Im linken Bildteil ist die Pyramide auch ohne explizite Beleuchtung hell erleuchtet, allerdings gleichmäßig aus allen Richtungen. In dieser Darstellung werden alle Teile/Seiten/Pixel der Pyramide mit der gleichen Helligkeit dargestellt. Reduziert man nun diese "allgemeine Helligkeit" und fügt eine explizite gerichtet Beleuchtung hinzu kommt auch die räumliche Tiefe stärker heraus (rechte Bildhälfte). (Die Pyramidentextur habe ich nebenbei seit dem letzten Tutorial von mexikanisch auf ägyptisch gewechselt; Texturkoordinaten ließen sich mit dem Foto in Kapitel 6 gut erklären, aber die Pyramidenform war nicht ganz sauber...) 7.1.1 Gerichtete Beleuchtung (directional lighting)Die gerichtete Beleuchtung von der hier die Rede ist, soll im Bild 7.2 verdeutlicht werden:Bild 7.2 : Gerichtete Beleuchtung Wie du in Bild 7.2 siehst, kann die hier vorgestellte gerichtete Beleuchtung am ehesten mit Sonnenlicht verglichen werden: parallele Lichtstrahlen kommen aus unendlicher Endfernung überall gleichmäßig verteilt an. Die Helligkeit, in der die Objektoberfläche erscheint, hängt von der Ausrichtung der Oberfläche zu den Lichtstrahlen ab. Je steiler das Licht auftrifft, desto heller erscheint das Objekt. D.h. bei dieser Form der simulierten Beleuchtung ist die Position des Betrachter zum Objekt nicht relevant. Man spricht von idealer diffuser Reflektion der Oberfläche. Die Oberflächenausrichtung wird durch den Vektor der Oberflächennormalen beschrieben: Bild 7.3 : Oberflächennormalen und Lichtrichtung Es entspricht der Erfahrung aus der realen Welt, dass die Helligkeit umso größer erscheint je kleiner der Winkel zwischen den Lichtstrahlen (rote Pfeile in Bild 7.3) und den Oberflächennormalen (grau in Bild 7.3) ist. Mathematisch wird dieser Zusammenhang über den Kosinus des Winkels beschrieben: cos(0°) = 1 (= 100% des Lichts wird reflektiert) cos(90°)= 0 (es wird kein Licht mehr reflektiert; die Lichtstrahlen streifen die Oberfläche nur noch) cos(>90°) lässt sich zwar noch berechnen, passt aber nicht zur Beleuchtungssimulation, daher wird bei der Berechung max(0,cos(α)) verwendet.7.1.2 Umgebungslicht (ambient lighting)Das Umgebungslicht ist wesentlich einfacher zu beschreiben als das gerichtete Licht. Es simuliert die unendlichen diffusen Reflektionen aller Lichtquellen der Umgebung. In der WebGL-Berechnung stellt sich das einfach als ein konstanter Mindestwert der Objekthelligkeit (unabhängig von irgendwelchen Lichtquellen) dar.7.1.3 Weitere BeleuchtungsartenIn diesem Kapitel soll es nur um die beiden erstgenannten Beleuchtungsarten gehen. Als kleiner Vorgriff und für das Gesamtverständis soll hier nur erwähnt sein, was es sonst noch gibt:
7.2 Licht in den Quellcode......zu bringen ist Ziel dieses Abschnitts. Nach den bisherigen Kapiteln erwartest du hoffentlich auch beim Thema Beleuchtung keinen WebGL-Befehl wieSetLight=1.0. Wir müssen auch hier wieder alles von Hand zusammensetzen.7.2.1 JavaScript-Teil (und HTML)In 7.1.1 habe ich bereits erklärt, dass für die gerichtete Beleuchtung die Oberflächennormale (Senkrechte) benötigt wird. D.h. wir müssen diese Normalen WebGL beibringen. Theoretisch kann man sie zwar mit ein bisschen Vektorrechnung aus den Punkten berechnen, aber zur besseren Übersicht, gebe ich sie hier noch explizit im Code an. Die FunktioninitBuffers() bekommt einen weiteren Buffer, der in ihr initialisiert wird:
pyramidVertexNormalBufferIDpyramidVertexNormalBufferID ist als globale Variable angelegt und wird nach dem gleichen Prinzip initialisiert wie bereits der triangleVertexPositionBufferID
und der pyramideTextureCoordBufferID.
Die Initialisierung geschieht in Z. 153f:
Die Normalen sind hier "von Hand" berechnet; Die vier Pyramidenwände stehen im 45° Winkel zur Horizontalen, daher gilt für die Einheitsnormalen, dass jeweils 2 Vektorkomponenten gleich Sqrt(0.5) ~= 0.707 und die dritte gleich 0 ist. Wenn dir das nicht gleich einleuchtet, rate ich zu Papier, Bleistift und Pythagoras. In drawScene(), Z.220/221 wird dann noch der Normal-Buffer an den Shader übergeben. Diese Verknüpfung zwischen dem Shader und dem JavaScript-Buffer wird in
glpsutilskap7.js, Z. 163 initialisiert:
Eine wichtige Komponente des gerichteten Lichts ist die NormalenMatrix nMatrix bzw uNMatrix.Wir haben die Normalen aller Vertices jetzt mit festen Werten initialisiert, was passiert aber wenn der User die Interaktionsmöglichkeiten WebGL-Szene nutzt und die Pyramide dreht oder verschiebt? Die Normalen müssen natürlich passend zur aktuellen Ausrichtung der Oberflächen neu berechnet werden und dies übernimmt die NormalenMatrix nMatrix bzw uNMatrix.Die vielleicht naheliegende Idee, hierfür einfach die ModelView-Matrix zu verwenden führt leider nicht weit: Die ModelView-Matrix beinhaltet Rotationen UND Translationen. Translationen würden sich auf die Normalenvektoren fatal auswirken, da sie deren Richtung ändern würden. Zur Veranschaulichung: Die Normalen sind immer auf den Punkt der zugehörigen Oberfläche, ihren "Ursprung", bezogen, egal wie diese Oberfläche im Raum verschoben wird. Noch "falscher" würde das Transformationsergebnis, sobald nicht-affine Transformationen (Skalierungen in eine Richtung, u.Ä.) hinzukommen. Daher muss für die NormalenTransformationsMatrix eine andere Herangehensweise gefunden werden. Der Weg zu dieser Matrix ist nicht ganz trivial, aber auf lighthouse3d gibt es eine sehr schöne Herleitung, die ich hier mit meinen eigenen Worten ins deutsche übertrage:
Gleichung (7.6) zur Berechnung der NormalenTransformationsmatrix ist in glpsutils7.js in der Funktion setMatrixUniforms implementiert (wieder mit Hilfe der Sylvester.js- Library):
Zum Shader selbst kommen wir später. Da das gerichtete Licht in diesem Beispiel noch über die Webseite veränderbar sein soll, fügen wir in der drawScene()-Funktion noch ein paar Zeilen hinzu, die die Werte der HTML-Formularfelder auslesen
und diese in den WebGL-Context übertragen. (kapitel7.html, Z.248f)
Ein Wort zur übertragung der Lichtrichtung aus dem Formular in den WebGL-Kontext: Der User der die Webseite benutzt, kann zunächst jeden beliebigen Wert in die Formularfelder eintragen. Eigentlich sollte noch eine Überprüfung stattfinden, ob "sinnvolle" Zahlenwerte eingegeben wurden, und ggf. eine Nachricht an den User gegeben werden, aber das habe ich mir hier gespart. Bei der Lichtrichtung ist es für die folgenden Vektorrechnungen erforderlich, dass der Richtungsvektor die Länge 1 hat. Man kann vom Benutzer der Webseite nicht erwarten, das explizit auszurechnen, daher wird mit der Funktion .toUnitVector aus der Sylvester-Bibliothek diese Normierung auf die Länge 1 nachträglich automatisch vorgenommen.An Ende von kapitel7.html sind zusätzlich die entsprechenden Formularfelder eingebaut. Wenn du bis hierher gelesen hast, brauchst du sowieso keine Erläuterungen zum <input>-Tag, also gibt's hier auch keine. (ansonsten hilft SelfHTML) 7.2.2 Fragment-ShaderIm Vergleich zu Kapitel 6 ist die Berechnung der Fragmentfarbe (gl_FragColor) auf zwei Zeilen verteilt.
Zuerst wird die Texturfarbe berechnet (unabhängig vom Licht). Danach wird dieser Farbwert mit einem 3-dimensionalen Vektor von Gewichtungsfaktoren ( vLightWeighting) multipliziert und in einem 4-dimensionalen Vektor gespeichert (zusammen mit dem Alpha-Transparenz-Wert).Woher kommen nun diese RGB-spezifischen Gewichtungsfaktoren ? Wie im Quellcode ersichtlich ist, wird vLightWeighting als varying vec3 zwischen den Shadern ausgetauscht bzw. vom Vertex-Shader an den
Fragment-Shader übergeben.Schauen wir uns also die Berechnung im Vertex-Shader an: 7.2.3 Vertex-ShaderDa die gerichtete Beleuchtung über das HTML-Formular komplett abschaltbar ist, wird in Z.48 eine Fallunterscheidung vorgenommen:
Im einfachen Fall (u_bUseLighting == false) werden die 3 Gewichtungsfaktoren auf 1.0 gesetzt, so dass das Licht sich effektiv nicht auswirkt. Im Fall der eingeschalteten Beleuchtung wird zunächst der NormalenVektor des Vertex mit der NormalenTransformationsmatrix transformiert. Danach wird mit dem dot(..)-Befehl das Skalarprodukt aus der transformierten Normalen und der Lichtrichtung fDirectionalLightWeighting
berechnet. fDirectionalLightWeighting wird mit der max Operation sichergestellt, das der Gewichtungsfaktor nicht kleiner als 0 wird.In der dritten Zeile des else-Zweigs wird der RGB-spezifische Gewichtungsvektor berechnet. Das Umgebungslicht (u_vAmbientColor) wirkt dabei unabhängig von irgendwelchen Gewichten oder Richtungen als konstanter Summand, während die Farben des gerichteten Lichts entsprechend der gerade berechneten Normalen-Ausrichtungen skaliert werden. Nochmal zur Erinnerung: diesen Lichtgewichtungsvektor vLightWeighting verwenden wir im Fragment-Shader (7.2.2) als Skalierungsfaktor für die Farbe bzw. Helligkeit.7.3 AusblickDas war dann wiedermal ein verhältnismäßig langes Tutorial zur Einführung der gerichteten Beleuchtung. Ich hoffe, du hast die wesentlichen Dinge verstanden. In einem der späteren Kapitel werde ich auf die weiteren (noch) komplexeren Varianten zum Thema Beleuchtung eingehen. Es gibt noch jede Menge zum Thema Punktbeleuchtung, Glanzeffekte/Reflexionen, Schattenwurf etc. zu entdecken.Es bleibt spannend! Inspiriert wurde dieses Tutorial von Giles Thomas' LearningWebgl.com. |